Formulas for building jumps

/14 Comments/in , , /by


Lee,

Is there a formula for figuring out the best height, length, curvature and angle of a jump to achieve the longest distance and height? And what would be the differences if you had the angle of the take off at say 35, 45 and 55 degrees?

Thanks, Brian

Hey Brian.

Of course there’s a formula! Actually, there are a bunch of formulas.

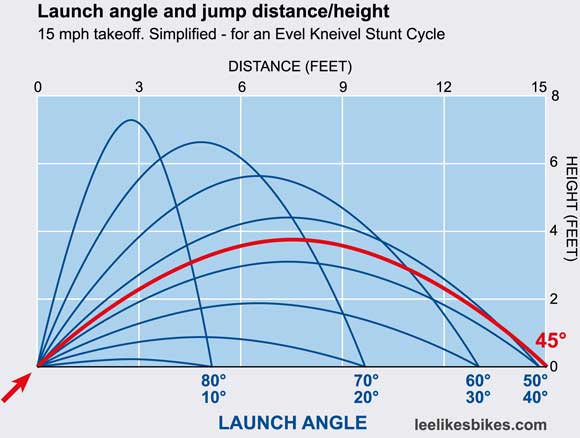
For the longest distance, you want a 45-degree lip.

If you carry 15 mph off a 45-degree lip, you’ll fly 15 feet beyond and 3.8 feet above the lip. On a 35-degree lip you’ll fly 14 feet out and only 2.5 feet up. On a 55-degree lip you’ll fly 14 feet (the same as the 35-degree lip) but fly twice as high: 5 feet.

For the greatest height, make the lip as steep as you can handle. At 15 mph, an 80-degree lip will launch you seven feet into the air. A vertical lip will shoot you 7.5 feet up, but you’ll land where you took off. Tricky.

Check out this chart action. 45 degrees gives you the most distance. As you get flatter, distance and height go down. As you get steeper, distance drops but height increases.

NOTE: This totally ignores suspension, technique and every other variable. You can make a jump tiny or huge by sucking it up or pumping it hard.

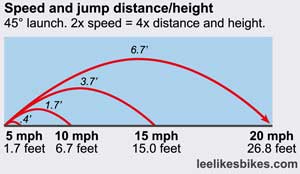
By the way, speed dramatically increases distance and height. 2x speed = 4x height and distance. Nifty!

For the equations and an online calculator, check out hyperphysics.phy-astr.gsu.edu

Length, height and curvature are trickier. You basically want to place the rider at the end of the ramp, at the proper launch angle, without subjecting him to forces he or she can’t handle. The details are too involved to reveal on this site (for free), but here are some basic ideas:

  • The farther or higher you want to go, the more speed you need.
  • The higher the speed, the longer and taller the jump must be. You need a smooth transition; otherwise you’ll crush your bike, and your eyeballs will rattle in your shoes.
  • If you’re going for distance, the angle will be about 45 degrees, the face will be low, and the curve will be gentle.
  • If you’re going for height, the angle will be 60 or more degrees, the face will be tall, and the curve will be tight.
  • If you’re going faster than you need to clear a gap, the angle will be 30 degrees or less, the face will be very low, and the curve will be very gentle.
  • Beginners need low faces, gentle curves (about 30 degrees) and low speeds.

    • Whew! I hope that helps. Email me if you want help designing a jump park.

    — Lee

    14 replies

    Comments are closed.